Schmetterlingsdiagramm - Wikipedia

In diesem Artikel werden Schmetterlingsdiagramme in FFT-Algorithmen behandelt. die gleichnamigen Sonnenfleckdiagramme finden Sie unter Sonnenzyklus.

Signalflussdiagramm, das die Eingänge x (links) mit den von ihnen abhängigen Ausgängen y verbindet (rechts) für einen "Schmetterlings" -Schritt einer radix-2-Cooley-Tukey-FFT. Dieses Diagramm ähnelt einem Schmetterling (wie der zum Vergleich gezeigte Morpho-Schmetterling), daher der Name, obwohl er in einigen Ländern auch als Sanduhrdiagramm bezeichnet wird.

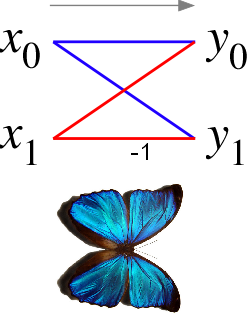
Im Zusammenhang mit schnellen Fourier-Transformationsalgorithmen wird ein Schmetterling genannt. ist ein Teil der Berechnung, bei der die Ergebnisse kleiner diskreter Fourier-Transformationen (DFTs) in eine größere DFT oder umgekehrt kombiniert werden (wobei eine größere DFT in Subtransforms zerlegt wird). Der Name "Schmetterling" kommt von der Form des Datenflussdiagramms im Fall radix-2, wie unten beschrieben. ^[1] Das früheste Vorkommen dieses Ausdrucks wird vermutlich in einem MIT-Bericht von 1969 (19659005) erwähnt ] Dieselbe Struktur kann auch im Viterbi-Algorithmus gefunden werden, der zum Finden der wahrscheinlichsten Folge verborgener Zustände verwendet wird.

Am häufigsten wird der Begriff "Schmetterling" im Zusammenhang mit dem Cooley-Tukey-FFT-Algorithmus verwendet, der rekursiv eine DFT mit zusammengesetzter Größe n = in zerlegt kleinere Umwandlungen der Größe m wobei der "Radix" der Umwandlung ist. Diese kleineren DFTs werden dann über Schmetterlinge der Grösse r kombiniert, die selbst DFTs der Größe r sind (durchgeführt m mal bei entsprechenden Ausgaben der Subtransformationen). vor multipliziert mit den Wurzeln der Einheit (bekannt als Twiddle-Faktoren). (Dies ist der Fall "Dezimierung in der Zeit"; man kann auch die umgekehrten Schritte durchführen, die als "Dezimierung in der Frequenz" bezeichnet werden), bei denen die Schmetterlinge an erster Stelle stehen und mit zwei Faktoren nachvervielfältigt werden. Siehe auch den Cooley-Tukey-FFT-Artikel .)

Radix-2-Schmetterlingsdiagramm [ edit ]

Im Fall des Radix-2-Cooley-Tukey-Algorithmus ist der Schmetterling einfach eine DFT der Größe 2, die zwei Eingaben aufnimmt ( x ₀ x ₁ ) (entsprechende Ausgaben der beiden Teiltransformationen) und gibt zwei Ausgaben ( y ₀ ] y ₁ ) durch die Formel (ohne Twiddle-Faktoren):

$1 {{displaystyle y_ {0} + x__ 1} ,}$

${ displaystyle y_ {1} = x_ {0} -x_ {1}. ,}$

Zeichnet man das Datenflußdiagramm für dieses Paar von Operationen, so ist das ( x ₀ x ₁ 1 bis ( y ₀ y ₁ ) Linien kreuzen sich und ähneln den Flügeln eines Schmetterlings, daher der Name (siehe auch Abbildung rechts).

Eine Dezimierungszeit-Radix-2-FFT bricht eine Länge von N DFT in zwei Längen N / 2 DFTs, gefolgt von einer Kombinationsstufe, die aus vielen Schmetterlingsoperationen besteht.

Genauer gesagt, ein Radix-2-Dezimierungszeit-FFT-Algorithmus über n = 2 ^p gibt Eingaben in Bezug auf ein Primitiv n Wurzel der Einheit ${\displaystyle {\mathrm{\omega \; <!--\; \omega \; -->}}_n^k=e^{-\; <!--\; -\; -->\frac{2\mathrm{\pi \; <!--\; \pi \; -->}ikn\mathrm{19659054]\; \{\; displaystyle\; omega\; \_\; \{n\}\; ^\; \{k\}\; =\; e\; ^\; \{-\; \{\; frac\; \{2\; pi\; ik\}\; \{n\}\}\}\}}}{}}}$ stützt sich auf O ( n log n ) Schmetterlinge der Form:

${\displaystyle y_0=x_0+x_1{\mathrm{\omega \; <!--\; \omega \; -->}}_n^k}$

${ displaystyle y_ {1} = x_ {0} -x_ {1} omega _ {n} ^ {k}, ,}$

wobei k eine ganze Zahl ist, abhängig vom berechneten Teil der Transformation. Während die entsprechende inverse Transformation mathematisch durchgeführt werden kann, indem ω durch ω ^-1 ersetzt wird (und möglicherweise mit einem Gesamtskalenfaktor multipliziert wird, abhängig von der Normalisierungskonvention), kann dies möglich sein auch direkt die Schmetterlinge umkehren: